N-Queens Problem

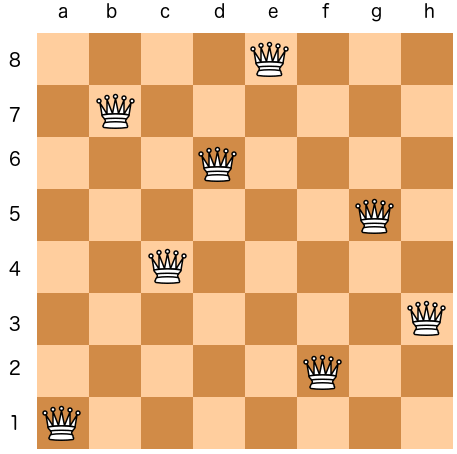
Our goal is to develop a solution to place N chess queens on an N×N chessboard so that no two queens threaten each other.

Algorithm

graph TD;
    A(Start) --> B(Initialize board);
    B --> C{All rows placed?};
    C -->|No| D{Try placing queen};
    D --> E{Safe placement?};
    E -->|Yes| F(Move to next row);
    F --> G{Solution found?};
    G -->|Yes| H(Print solution);
    G -->|No| D;
    E -->|No| I(Backtrack);
    I --> J{All columns tried?};
    J -->|Yes| K(Backtrack to previous row);
    J -->|No| D;
    C -->|Yes| L(No solution exists);
    H --> M(End);
    L --> M;
    K --> D;

---

Here is the entire code for you to try

def IsSafe(board, row, col):
    for i in range(row):
        if board[i] == col or board[i] - i == col - row or board[i] + i == col + row:
            return False
    return True

def Solution(board, row):
    if row == len(board):
        return True
    for col in range(len(board)):
        if IsSafe(board, row, col):
            board[row] = col
            if Solution(board, row + 1):
                return True
            board[row] = -1
    return False

def NQueens(n):
    board = [-1] * n
    if Solution(board, 0):
        for i in range(len(board)):
            for j in range(len(board)):
                if board[i] == j:
                    print("Q", end=" ")
                else:
                    print(".", end=" ")
            print()
    else:
        print("No solution exists")

NQueens(9)

Output

Q . . . . . . . 
. . . . Q . . . 
. . . . . . . Q 
. . . . . Q . . 
. . Q . . . . . 
. . . . . . Q . 
. Q . . . . . . 
. . . Q . . . .